Every once in a while you get fixated on something and the only way to let it go is to share it with others. So …. while reviewing the logical IF function and nested IF statements, I came up with a chart or table, that sort of evolved out of curiosity.
It started by looking at two conditions, both having true or false possibilities, as shown in the table below, where A and B have four possible outcomes.
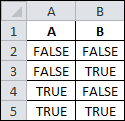
If you type the lowercase true or false into a cell they will change to uppercase TRUE or FALSE. That’s because Excel interprets them as logical functions.
You can also type =TRUE() or =FALSE() to get the same thing. Both functions have no arguments, yet return the logical values TRUE and FALSE, respectively.
 Also take notice that text values align to the left side of a cell, numbers to the right, but logical values align to the middle.
Also take notice that text values align to the left side of a cell, numbers to the right, but logical values align to the middle.
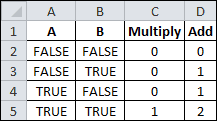 TRUE and FALSE both have numerical values that you can see when mathematical operations are performed on them. In the table to the right, multiplying A times B gives values of zero (0) or one (1), but adding A and B gives values of zero (0), one (1), or two (2). Which proves that TRUE = 1 and FALSE = 0.
TRUE and FALSE both have numerical values that you can see when mathematical operations are performed on them. In the table to the right, multiplying A times B gives values of zero (0) or one (1), but adding A and B gives values of zero (0), one (1), or two (2). Which proves that TRUE = 1 and FALSE = 0.
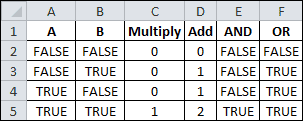
When the outcomes for A and B are used as arguments for the AND and OR functions, it gives you a sense for the rules of how they operate.
The AND function will return TRUE if all of its logical arguments evaluate to TRUE. In this example, observation shows this to be the same as multiplying A and B together, given the numerical values of TRUE (1) and FALSE (0).
The OR function returns TRUE if any argument is TRUE, and returns FALSE if all arguments are FALSE.
Another logical function is NOT, which simply reverses the value of its logical TRUE or FALSE argument. Using AND inside the NOT function gives us the reverse of the AND function and is know as NAND. (see chart below)
Using the OR function inside the NOT function is called NOR and gives us the reverse of the OR function, as shown.
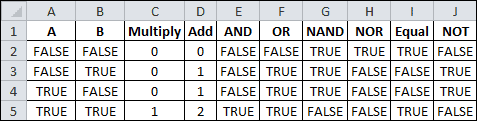
Finally, using an equals (=) comparison between A and B is done to come up with a completely different set of TRUE and FALSE values for these four outcomes. It shows if A and B are the SAME.
Using the Equal comparison inside the NOT function gives us the reverse values, or not the same.
You can now put this completely out of your head and get on with your life.
